Graph - Max-flow

Created:2019-02-24  Last modified:2019-02-24

  1. Introduction

    Max-flow problem

    1. Input: a flow network, which includes a graph (V,E), positive integer edge capacities and a source vertex s, a target vertex t.
    2. Goal: find a maximum flow from s to v (The maximum flow can use multiple paths, which differs from the maximum bottleneck program [The widest path problem].)
    3. Constraints: each edge's flow inside [0, edge-capacity];
      for all vertex except s and t, input flow = output flow

    Anti-parallel edges

    To simplify algorithm, we suppose there does not exist parallel edges. If exists, using the following method to remove one edge.

  2. Ford-Fulkerson Algorithm

    Concept

    1. Flow network (defined before)
    2. Flow (f): based on the residual network, find one augmenting path. Add this augmenting path to the pervious flow. (A flow network exists multiple possible flows)
    3. Available capacity network: after reduce the use flow from the flow network, the remaining capacity construct a avaliable network
    4. Residual network (G_f): Remove the 0 flow edge from the avaiable capacity network, and create reverse edge with capacity equals to assigned flow from the flow.
    5. Example

    6. st-path: a path from the source vertex s to the target vertex t.

    Algorithm

    1. Initialized a flow network with each edge of flow = 0
    2. Generate available capacity network based on Input Network and Flow network
    3. Generate residual network based on avaliable capacity network and flow network
    4. Run DFS or BFS on the residual network to find a st-path.If no path found, return
    5. Find the minimum edge weight along this st-path. Suppose it is w.
    6. Update (Augment) the flow network with the w on the st-path.
      ** If the used edge has the same direction on the original flow, the increase. Otherwise decrease.
    7. Repeat step 2.

    Runtime

    Each iteration will increase the flow by at least one unit. Each iteration takes O(|V + E|) = O(E). The max-flow size is C. So O(|E|*C).
    pseudo-polynomial runtime: The runtime is depends on the input.

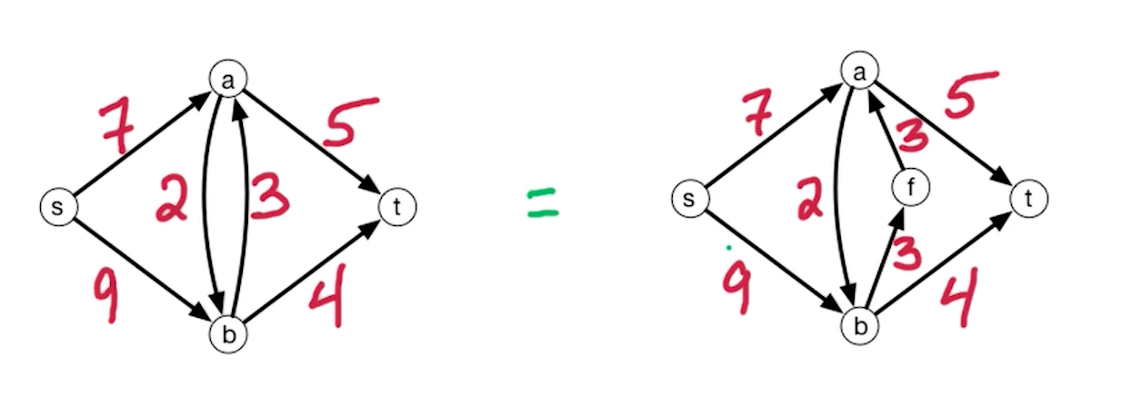
  3. Min-cut=Max-flow

    Concepts

    1. Min-cut=Max-flow: The size of max-flow on a flow network is the min-cut capacity of the st-cut.
    2. A cut (L, R) is a partition of V = L U R.
    3. st-cut: The cut is identified by the vertex s and vertex t, where are the source and target of the flow-network.
    4. Capacity(L,R): sum of weight of all out-edges from L to R

    size(f) = f_out(L) - f_in(L)

    Size of a flow is the out-flow across the cut substracts the in-flow across the cut.

    Intution: size(f) = f_out(s), f_in(s) = 0; all other vertices except s and t have f_in = f_out

    size(f*) = cap(L,R)

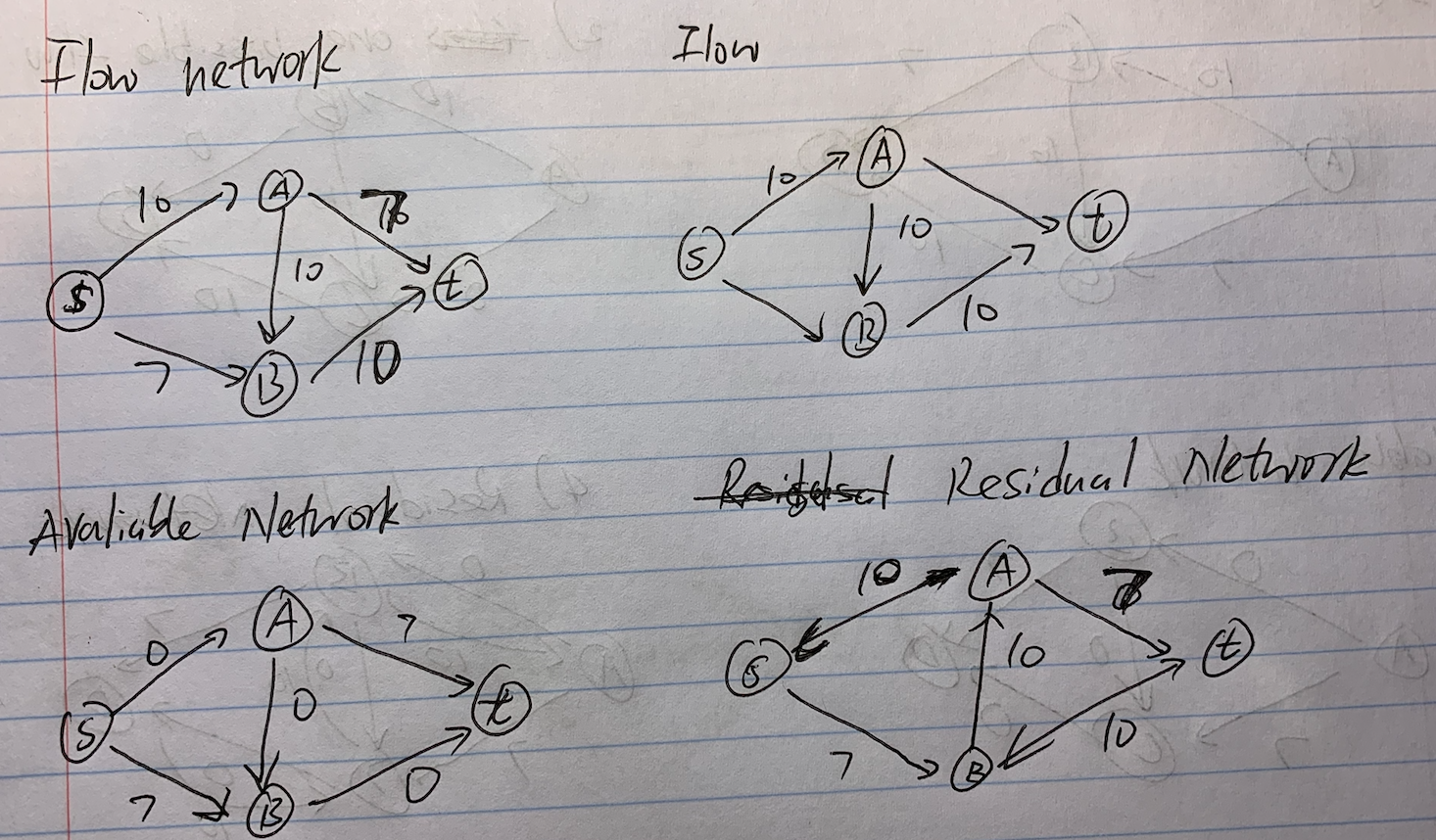
    1. f* is generate by Ford-Fulkerson algorithm so we have there does not exist a st-path on the residual network.(1)
    2. The out-edge across from L to S must disappear in the residual network, otherwise it violates (1). If an edge disappear in the residual network, it means it is fully occupied. So f*_out(L) = sum(out-edge weight) = cap(L,R)
    3. The in-edge across from L to S must have flow 0 otherwise, it has create an out-edge from L to S in the residual network, which violates (1). So f*_in(L) = 0
    4. Therefore, size(f*) = f*_out(L) - f*_in(L) = cap(L,R)

    Proof

    I. max size(f) <= min cap(L,R)

    max-flow <= min st-cut is equalient to any flow <= any st-cut
    size(f) = f_out(f) - f_in(L) <= f_out(f) <= cap(L,R)

    II. max size(f) => min cap(L,R)

    Because max flow(f) >= size(f*) = cap(L,R) >= min cap(L,R), we have max size(f) => min cap(L,R)
    Even though we know ford-fulkerson can generated the max-flow, but since we did not prove, so we have max-flow >= f*

  4. Edmonds-Karp Algorithm

  5. References

    1. Udacity CS6505 Gatech Algorithm