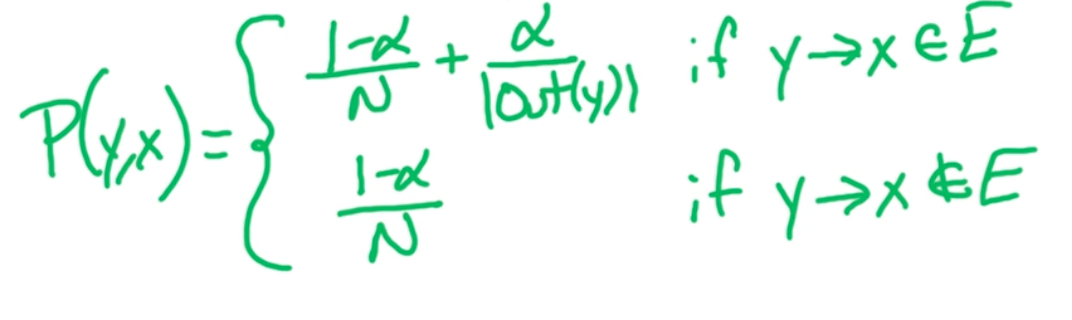Graph - Markov Chains

Created:2019-02-18  Last modified:2019-02-18

  1. Introduction

    Markov Chains (wiki): a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.

    This model can be represented by a connected directed graph, edge' weight is the probability to shift to next state (vertex) from the current state (vertex)

    Time is discrete, each time is one move

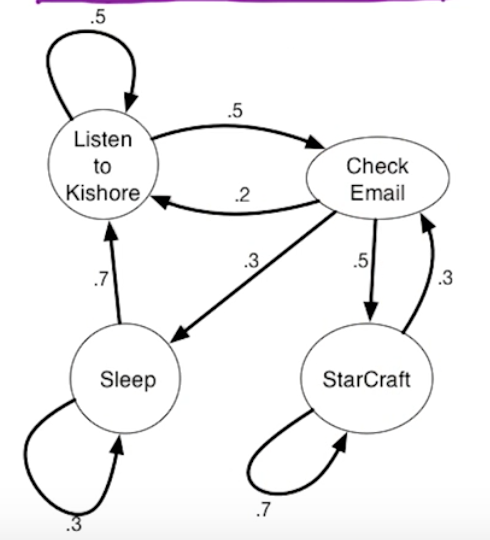
    The sum of out edge on a vertex is 1

    Matrix representation of the graph, it is also called transition matrix, P(i,j) = Pr(i->j) = Pr (next = j | current = i)

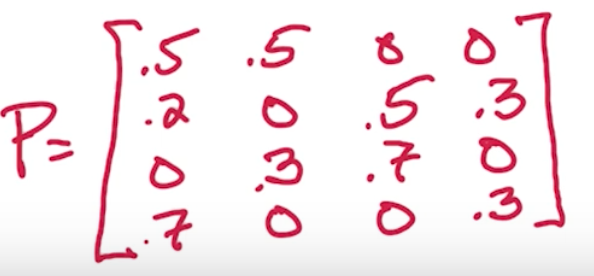
    Properties of the transition matrix

    1. P is a stochastic matrix: each row's sum = 1 (If column's sum is also 1, then P is a doubly stochastic)
    2. N-step transition: P^N is the distribution after moving N steps (N time)
      e.g. 2-step P^2. P^2(check-email -> star-craft) = P^2(2, 3) = 0.35 = 0.5 * 0.7
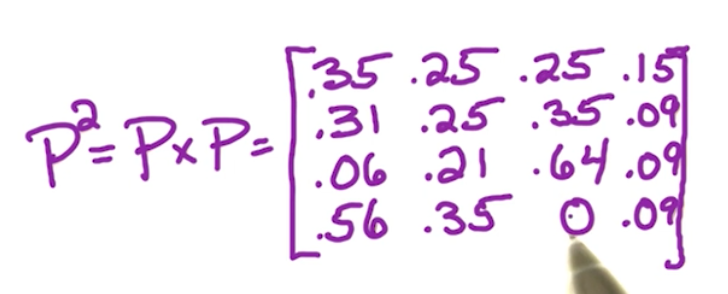
    3. Infinite Time: when P becomes larger and larger, P^N converage (unchanged) and row are the same. It means no matter where you start, the probability of ending at a state is same.

      π is a stationary distribution
    4. π is an eigenvector with eigenvalue = 1
      distribution at (t) * P = distribution at (t+1). For a stationary distribution, we have πP = π. So π is an eigenvector with eigenvalue = 1

    Unique stationary distribution

    Ergodic Markov Chain, aperiodic & irreducible, has one unique stationary distribution

    1. Counterexample that markov chains have a periodical structure: e.g. A bipartite markov chains
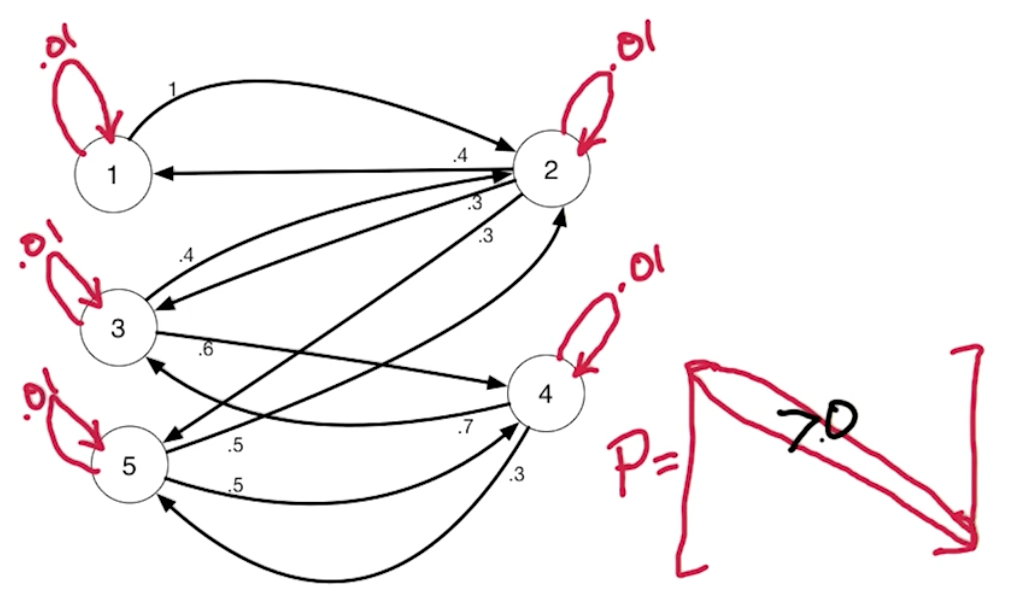
    2. Eliminate the periodical strcuture by letting matrix's diagonal > 0
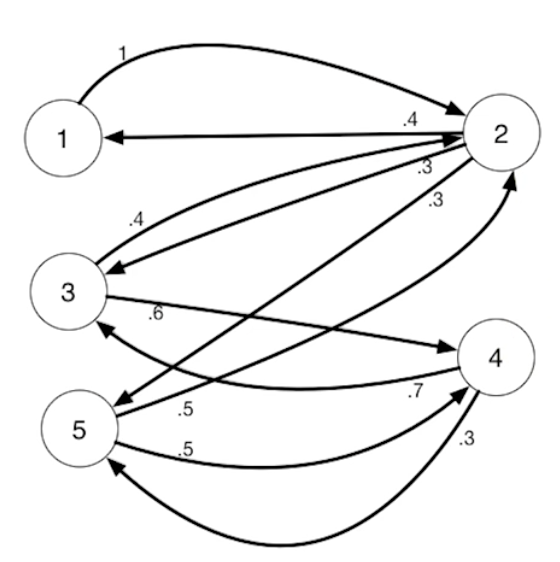
    3. Counterexample that markov chains have multiple SCC: e.g. starting from a sink SCC never reaches other SCC
    4. Make sure markov chains is irreducible, namely, only one SCC. To do this, manully add a tiny weigth edge between any two vertices that are not connected.

  2. PageRank

    PageRank is an algorithm to give each webpage (url) a quantity of its "importance". And the importance is used to sort webpages to make sure the webpages are shown in the order of relevance.

    Each page is a vertex, each hyperlink is a edge

    Webgraph

    1. each webpage is a vertex, each hyperlink is an edge
    2. π(x) is the rank (importance) of x
    3. Out(x) is out-neighbors of x
    4. In(x) is in-neighbors of x
    5. Intuitive method: the importance of a webpage = how many webpages cite this webpage #In(x), how many webpages In(x) cite, how important are In(x).
      A webpage cites 1000 webpages, which includes p1. A webpage only cites p2. p2 is famous than p1.
      =sum 1/out(y) over y in In(x)
      A infamous webpage only cites p1, a CNN webpage cites 1000 webpages which include p2. p2 is famous than p1.
      =sum π(y)/out(y) over y in In(x)
    6. Random walk method: start from a webpage, equally randomly select a hyperlink to go to the next page. In order word, Pr(from page y to page x) = Pr(y - > x) = 1/out(y). We can use this to construct a markov-chain transition matrix.

    Webgraph stationary distribution

    1. The webgraph may have multiple SCC.
    2. Make sure a stationary distribution: add an random edge (hyperlink) on each node (webpage)
      select a damping factor a, (0 < a <=0). With a probability, we will use the original transition. 1 - a probability to use the random edge. (Google use a = 0.85, a = 0 when the node is a sink node)
      smaller a faster converagence
      bigger a more precise.
    3. Erogic MC

  3. References